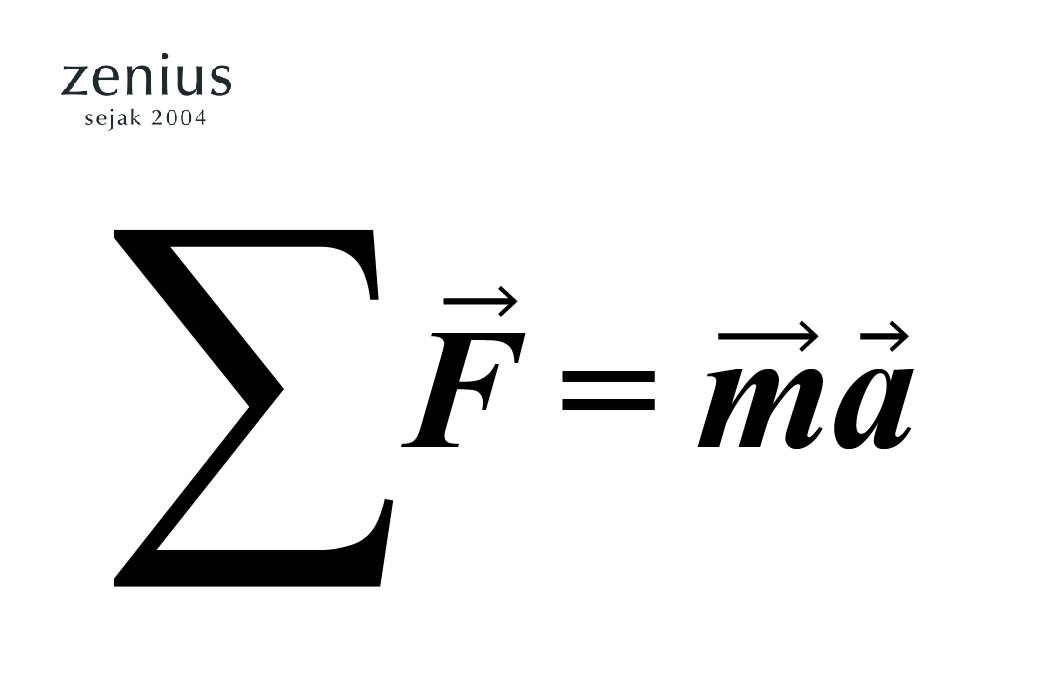Hukum Newton adalah hukum yang menggambarkan hubungan antara gaya yang bekerja pada suatu benda dan gerak yang disebabkannya.Agar kamu memahami materi Hukum Gerak Newton dengan baik, kamu harus memahami terlebih dahulu gerak lurus.
Hukum Newton 1“Setiap benda akan mempertahankan keadaan diam atau bergerak lurus beraturan, kecuali ada gaya yang bekerja untuk mengubahnya”.(https://www.zenius.net/blog/23205/materi-hukum-newton-12-dan-3-beserta-contoh-soalnya)
Contoh Soal Benda diam, hitunglah gaya normal yang bekerja pada benda!
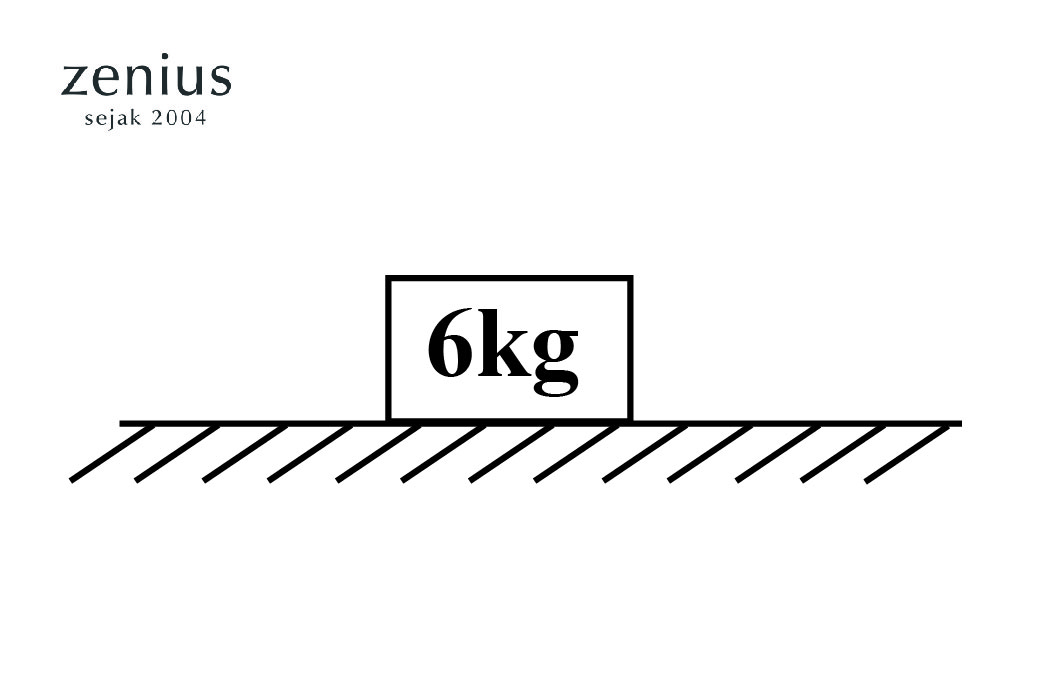 Pembahasan:
Pembahasan:
m = 6 kg
g = 10 m/s2
W = m . g
= 6 x 10
= 60 N
Dari contoh soal, kita dapat mengetahui bahwa berat (W) berat dipengaruhi oleh gaya gravitasi dan gaya normal (N) selalu tegak lurus ke permukaan yang bersentuhan dengan benda. Perhatikan gambar berikut.

sumber gambar.((https://www.zenius.net/blog/23205/materi-hukum-newton-12-dan-3-beserta-contoh-soalnya)
Sehingga,
N – W = 0
N – 60 = 0
N = 60 N
Bunyi: “Jika resultan pada suatu benda sama dengan nol, maka benda yang diam akan tetap diam dan benda yang bergerak akan tetap bergerak dengan kecepatan tetap”.
Berdasarkan hukum ini, kamu dapat memahami bahwa suatu benda cenderung mempertahankan keadaannya. Benda yang diam akan cenderung untuk tetap diam dan benda yang bergerak akan cenderung untuk tetap bergerak. Oleh karena itu, Hukum Newton I juga disebut sebagai hukum kelembaman atau hukum inersia.
Contoh penerapan Hukum Newton I dapat kamu amati apabila kamu sedang dalam kendaraan yang sedang bergerak kemudian direm secara mendadak, maka badan kamu akan terdorong ke depan. Itulah yang dimaksud dengan “kecenderungan untuk tetap melaju”.
Contoh lainnya dapat kamu amati apabila kamu sedang duduk pada kendaraan yang diam kemudian bergerak secara mendadak, maka badan kamu akan tersentak ke belakang. Itulah yang dimaksud dengan “kecenderungan untuk tetap diam”.
contoh lainnya Jika meletakkan misalnya koin pada atas kain kemudian kain tersebut di Tarik secara cepat, maka koin tersebut akan tetap.(https://rumus.co.id/hukum-newton/)
Contoh-contoh diatas merupakan peristiwa kelembaman atau inersia. Sifat kelembaman suatu benda ditentukan oleh massa benda tersebut. Makin besar massa benda, maka kelembamannya akan semakin besar.
Massa merupakan besaran inersia suatu benda. Semakin besar massa suatu benda, maka akan semakin besar gaya yang dibutuhkan untuk membuat benda tersebut melakukan akselerasi atau percepatan. Selain itu, massa benda yang besar akan lebih susah untuk digerakkan dari posisi diam dan susah dihentikan dari kondisi bergerak.
Hukum Newton 2
Bunyi: “Percepatan sebuah benda berbanding lurus dengan gaya total yang bekerja padanya dan berbanding terbalik dengan massanya. Arah percepatan sama dengan arah gaya total yang bekerja padanya”.
Berdasarkan Hukum Newton II, kamu dapat memahami bahwa suatu benda akan bertambah kelajuannya jika diberikan gaya total yang arahnya sama dengan arah gerak benda. Akan tetapi, jika arah gaya total yang diberikan pada benda tersebut berlawanan dengan arah gerak benda maka gaya tersebut akan memperkecil laju benda atau bahkan menghentikannya.
Karena perubahan kelajuan atau kecepatan merupakan percepatan. Maka dapat disimpulkan bahwa gaya total yang diberikan pada benda dapat menyebabkan percepatan. Contoh penerapan hukum Newton II dapat kamu amati apabila kamu menendang sebuah bola (artinya kamu memberikan gaya kepada bola), maka bola tersebut akan bergerak dengan percepatan tertentu.
Hukum Newton II dinotasikan dengan rumus:
Dimana:
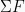 = gaya total yang bekerja pada benda (N)
= gaya total yang bekerja pada benda (N)
 = massa benda (kg)
= massa benda (kg)
 = percepatan benda (m/s2)
= percepatan benda (m/s2)
dikutip dari https://www.studiobelajar.com/hukum-newton-1-2-3/
Contoh soal:
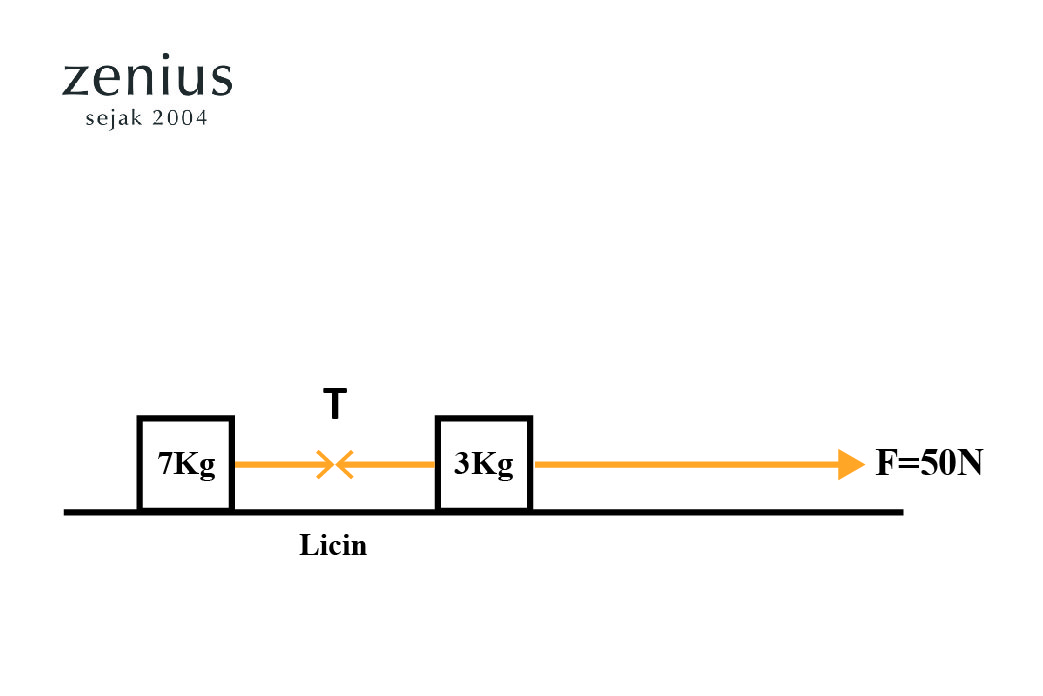
Perhatikan gambar berikut.
sumber gambar (https://www.zenius.net/blog/23205/materi-hukum-newton-12-dan-3-beserta-contoh-soalnya)
Pembahasan:
Berapakah percepatan benda?
Berapa tegangan tali?
ma = 7 kg
mb = 3 kg
F = 50 N
Pada benda A, terdapat gaya tegangan tali (T) ke kanan.
Karena
T = 7 . a ….(i)
Pada benda B, terdapat gaya tegangan tali (T) ke kiri dan F = 50 N ke kanan
Sehingga,
50 – T = 3 . a ….(ii)
Dari persamaan i dan ii, kita eliminasi untuk mendapatkan nilai a
T = 7a
50 – T = 3a
50 - (7a) = 3a
50 = 10a
a = 5 m/s2
Selanjutnya, substitusi nilai ke salah satu persamaan untuk mendapatkan nilai T
T = 7a
= 7 . 5
= 35 N
Jadi percepatan benda sebesar 5 m/s2 dan tegangan tali sebesar 35 N
Hukum Newton 3
Bunyi: “Ketika suatu benda memberikan gaya pada benda kedua, benda kedua tersebut memberikan gaya yang sama besar tetapi berlawanan arah terhadap benda pertama.”
Contoh penerapannya adalah saat kamu memukul meja (artinya memberikan gaya kepada meja), maka meja tersebut akan memberikan gaya kembali kepada tangan kamu dengan besar yang sama dan berlawanan arah dengan arah gaya yang kamu berikan. Oleh karena itu, semakin besar kamu memukul meja, maka tangan kamu akan semakin sakit karena meja melakukan gaya yang juga semakin besar ke tangan kamu.
1. Jelaskan bunyi hukum newton 1!
2. Jelaskan bunyi hukum newton 2 !
3. Jelaskan bunyi hukum newton 3 !
4. Tuliskan rumus Hukum newton 1, 2 dan 3 !
5. Contohkan yang termasuk hukum newton 1 !
6. Contohkan yang termasuk hukum newton 2 !
7. Contohkan yang termasuk hukum newton 3 !